質數(Prime number),又稱素數,指在大于 的自然數中,除了 和該數自身外,無法被其他自然數整除的數(也可定義為隻有 與該數本身兩個正因數的數)。
如何快速判斷某個數是否為質數?如何再給定區間内篩出所有的質數?
以上兩個問題是大廠面試官常常喜歡考察的。本文采用多種思路,對以上兩個問題進行簡析。
本文所有的函數參數均默認為自然數。
文章所涉及的代碼使用C 語言,使用的缺省源如下:
#include<cstdio> #include<ciso646> namespaceMain{ namespaceSource{ typedefshortunsignedinthu; typedefunsignedintuint; typedeflonglongunsignedintllu; } usingnamespaceSource; staticinlineconstvoidmain(){} } signedintmain(){Main::main();return0;}
問題1:素數判斷判斷一個非負整數 是否為質數。
解決方案 1.1根據定義,可以寫出如下代碼:
staticinlineconstboolisprime(constuinta){ if(a==0ora==1)returnfalse; for(registeruinti(2);i<a; i)if(not(a%i))returnfalse; returntrue; }時間複雜度 ,空間複雜度 , 内約可以解決 的問題。
解決方案 1.2考慮優化。
我們觀察一下一個合數 會被哪個數篩掉。可列出下表(記為表 1):
篩掉 的數42628293102122142153162182202213222242255262
(左側為 ,右側為篩掉 的數。)
核心代碼:
static inline const uint mpf(const uint c) { for (register uint i(2); i < c; i) if (not(c % i)) return i; return 0;}
發現篩掉 的數都較小,我們想到,如果在一個比較小的範圍内沒有 的約數,那是否可以判斷 是質數呢?
于是,我們考慮找到一個合數 的最小非 因數的上限。
設 為一個合數,令 為 的最小非 因數,令 ,顯然 。
由于 為合數,故 ,故 ,而 為 的最小非 因數,故 。
故 ,。
所以,若 為合數,則 必定有一個不大于 的因數;若 中沒有 的因數,則 為質數( 除外)。
所以枚舉到 即可。
staticinlineconstboolisprime(constllua){ if(a==0ora==1)returnfalse; for(registeruinti(2);1ull*i*i<=a; i)if(not(a%i))returnfalse; returntrue; }時間複雜度 ,空間複雜度 , 内約可以解決 内的問題。
問題2:區間内篩選素數篩出 中的質數,得到一張 的質數表。
解決方案 2.1可以通過上面 1.2 中的代碼判斷每個數是否是質數。
staticinlineconstboolisprime(constllua){...} enum{N=1u<<20}; staticuintn; staticboolisp[N]; staticuintprime[N],cp; staticinlineconstvoidmain(){ scanf("%u",&n); for(registeruinti(0);i<n; i)if(isp[i]=isprime(i))prime[cp ]=i; for(registeruinti(0);i<cp; i)printf("%u\n",prime[i]); }時間複雜度 ,空間複雜度 ,由于大部分數為合數,常數較小, 内約可以解決 的問題。
解決方案 2.2觀察表 1,我們發現,篩掉合數的數總是質數。
于是我們猜想:一個合數 的最小非 因數為質數。
證明:若 的不為 的最小因數為 且 并非質數,則 必然有約數 滿足 ;此時必然有 ,又 ,故 且 ,與 是 的最小非 因數矛盾。得證。
于是可以優化一下 isprime 函數。
enum{N=1<<24}; staticuintn; staticboolisp[N]; staticuintprime[N],cp; staticinlineconstboolisprime(constllua){ if(a==0ora==1)returnfalse; for(registeruinti(0);i<cpand1ull*prime[i]*prime[i]<=a; i) if(not(a%prime[i]))returnfalse; returntrue; } staticinlineconstvoidmain(){ scanf("%u",&n); for(registeruinti(0);i<n; i)if(isp[i]=isprime(i))prime[cp ]=i; for(registeruinti(0);i<cp; i)printf("%u\n",prime[i]); }時間複雜度 (由素數定理 中素數密度約為 ),空間複雜度 , 内約可以解決 的問題。
圖中的曲線分别表示質數數量 pi(n)(藍)、n / ln n(綠)與 Li(n)(紅)。
解決方案 2.3既然可以用質數判斷一個數是否為合數,那為什麼不直接用質數篩出合數呢?這樣可以減少很多不必要的計算吧。
容易想到,我們從 開始枚舉,用 isp[i] 表示 之前有沒有被篩過,若枚舉到一個數未被篩過,則其為質數,用之篩去後面的合數。
enum{N=(constuint)4e7}; staticuintn; staticboolisp[N]; staticuintprime[N],cp; staticinlineconstvoidmain(){ scanf("%u",&n); for(registeruinti(0);i<n; i)isp[i]=true;isp[1]=isp[0]=false; for(registeruinti(0);i<n; i){ if(isp[i]){ prime[cp ]=i; for(registeruintj(i);j<n;j =i)isp[j]=false; } } for(registeruinti(0);i<cp; i)printf("%u\n",prime[i]); }時間複雜度 ,空間複雜度 , 内約可以解決 的問題。
這種方法被稱為埃氏篩(埃拉托斯特尼篩法,sieve of Eratosthenes),是一種非常經典的入門篩法。
時間複雜度直觀證明:
假設素數在區間内按照質數定理的結論均勻分布,将求和轉化為積分,可得計算次數約為
解決方案 2.42.3 的主要缺點是合數被篩出多次,造成時間複雜度偏大。
考慮使每個合數 被其最小質因數篩掉。
設大于 的正整數 的最小質因數為 (若 為質數顯然有 ),定義 。
考慮枚舉素數 和大于 的正整數 ,使得 (此時顯然 )。
那麼,如果我們能找到一種方法枚舉出所有這樣的數對 ,我們就可以篩出所有合數(即 )。
比較顯然地,有 ,故 等價于 。
于是,我們枚舉滿足 為質數且 的數對 即可。
考慮枚舉 ,發現确定 後 不太容易枚舉。
于是考慮枚舉大于 的正整數 ,确定 後枚舉質數 ,使得 。
我們确定 後從小到大枚舉質數 ,則第一個滿足 的質數 即為 ,此前枚舉到的 均滿足 。
于是可以寫出如下代碼:
enum{N=(constuint)2e8}; staticuintn; staticboolisp[N]; staticuintprime[N],cp; staticinlineconstvoidmain(){ scanf("%u",&n); for(registeruinti(0);i<n; i)isp[i]=true;isp[1]=isp[0]=false; for(registeruinti(2);i<n; i){ if(isp[i])prime[cp ]=i; for(registeruintj(0);j<cpand1ull*i*prime[j]<n; j){ isp[i*prime[j]]=false; if(not(i%prime[j]))break; //注意到這裡枚舉到了首個滿足 i mod prime[j]=0的 j,不能簡單地将判斷移至 for 語句中。 } } for(registeruinti(0);i<cp; i)printf("%u\n",prime[i]); }時空複雜度 , 内約可以解決 的問題。
這種方法被稱為線性篩法(歐拉篩法,sieve of Euler),是一種非常常用的篩法。
由于這種方法可以方便地區分篩掉合數的兩個數之間是否存在倍數關系,故常常可用來篩積性函數。
好了,關于質數的一系列面試問題我們就聊到這裡,記得點贊哦~~
,
數學面試試講容易出的題目
更新时间:2025-07-06 21:16:58
Comments
Welcome to tft每日頭條 comments! Please keep conversations courteous and on-topic. To fosterproductive and respectful conversations,
you may see comments from our Community Managers.
Sign up to post
Show More Comments
相关案例
推荐阅读

隻身一人到你的城市
突然接到任務要陪領導出差,我有點小激動,因為想着你就在這個城市。在途中的路上,我猶豫再三還是發了個信息給你:我來到了你的城市,你可否有空見下我?其實我的城市與你的城市相隔隻不過三小時而已的車程,但我已記不得我們上一次見面是多少年前的事了?我...
2025-07-06
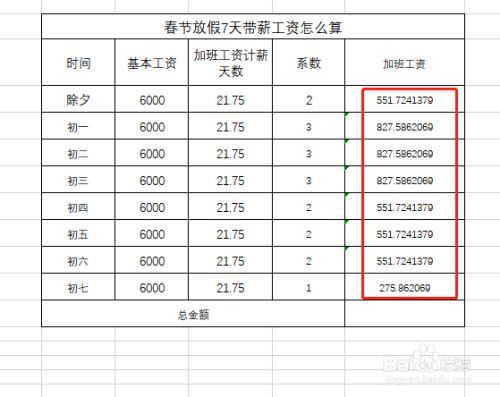
基本工資怎麼算
基本工資怎麼算?基本工資的算法如下:制度工作時間的計算,年工作日為365天減104天(休息日)減11天(法定節假日)等于250天季工作日為250天除以4季等于62.5天/季月工作日為250天除以12月等于20.83天/月工作小時數的計算是以...
2025-07-06

面試要注意問哪些問題
面試要注意問哪些問題?了解,在面試之前,肯定需要詳細了解你選擇的崗位我覺得在剛剛選擇職業之前,不要太在意工資的多少,主要是看看是否适合自己這個很重要是否有利于自己的成長,如果你在公司幹的好,公司是會給你漲工資的最開始還是多了解崗位的性質以及...
2025-07-06

員工工作定級測評表
崗位定級不僅将崗位細化分工細化也有助于體現勞動成果和價值的關系《員工定崗定級.xls》19份員工定崗定級資料文末附資料下載方式No.1資料詳情本套資料包含定崗定級管理辦法、崗位等級及入職定薪定級表、崗位分類、定崗定級考核表、行政部薪資定級及...
2025-07-06

每周工作五天輪休制是什麼意思
每周工作五天輪休制是什麼意思?一周工作五天這個職位有兩個人這星期他們得休息另一方必須值班下星期,該輪到休息了他們值日,下面我們就來聊聊關于每周工作五天輪休制是什麼意思?接下來我們就一起去了解一下吧!每周工作五天輪休制是什麼意思一周工作五天。...
2025-07-06












